Deep contextual multi-armed bandits: Deep learning for smarter A/B testing on autopilot

The machine learning team at HubSpot recently published a paper which we presented at the Uncertainty in Deep Learning Workshop at the Uncertainty in Artificial Intelligence conference. In this paper, we outlined how we’re using machine learning to help our customers do better A/B testing in HubSpot. This technology is now available in HubSpot’s Lead Flows tool, and we’ll soon roll it out to many other areas of the product. In this post, we’ll explain how the technology works and how it will help our users accomplish A/B testing with less effort and higher returns.

The Problem with A/B Testing

A/B testing is a widely used marketing technique. For example, a marketer might have a few different ideas for what text to display in an advertisement. Instead of blindly guessing, she instead decides to test the versions and see which one performs best. For a period of time, users are randomly shown the different versions of the ad. Once the marketer sees which ad has received the most clicks, she can choose to use that version from now on.

HubSpot’s product has offered tools to do traditional A/B testing for quite some time. But there are two big problems with A/B testing, problems that make A/B testing difficult to use in practice and leads to money left on the table:

1. The A/B test user has to decide which version of the advertisement is best after a period of time. But that’s not always so easy — often it’s hard to tell whether the difference between the variations is due to randomness or because one variation is truly better than the other.
   
   HubSpot’s Machine Learning team has an effective solution to this problem: Multi-armed Bandits (MAB). MABs allow you to run a test continuously, eventually converging to the correct version automatically. This allows our users to set up an A/B and let HubSpot do the rest.
2. Even if most users prefer version A to version B, a smaller (but important) segment might actually prefer version B. For example, suppose that 70% of your traffic is from the United States and 30% is from outside of it. Maybe customers in the US prefer version A, but international customers prefer version B. If you happen to decide to use version A because it performed best overall, you’d be leaving money on the table from your international audience.

Our work addresses both of these problems:

Set-and-Forget A/B Testing

There’s a large subfield of research on MABs. But one simple approach to MABs that works well in practice is called Thompson sampling.

Say you run an A/B test for 1,000 iterations, and both variations get sent to 500 users each. 105 click on variant A, and 100 click on variant B. In this case, A seems better, but not by much. Maybe A happened to be sent to more users who were likely to click on it — or maybe A genuinely is better.

If we think A is genuinely better, we should exploit that knowledge by showing A to more and more users. But if there’s a still chance that B is better, we want to learn more about B’s performance. So, we should still show B sometimes too. This is the classic exploration vs. exploitation trade-off. We want to make use of what we know about the good variants and also explore variants we still aren’t sure about.

We can use probability theory to quantify our uncertainty about the likelihood to click of each variant. In particular we construct probability distributions p(click | show A) and p(click | show B). In order to trade-off between exploration and exploitation using Thompson sampling, each time we’re asked which variant to show, we take a single sample from each probability distribution and show the one with the highest probability of clicking. If we are very confident one variant is clearly better, then that variant will almost always be shown. If our probability distributions are flat (or uncertain), we will show both variants in similar proportions.

Below, we simulate data from an A/B test in which the true p(click | show A) = 0.6 and p(click | show B) = 0.4, meaning that A is clearly the better variant. In the below animation, we can see how the estimated/learned probability distribution changes over time and becomes more certain that A is better.

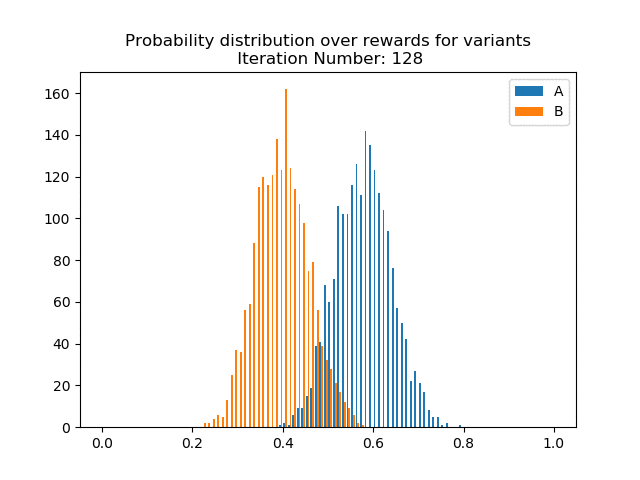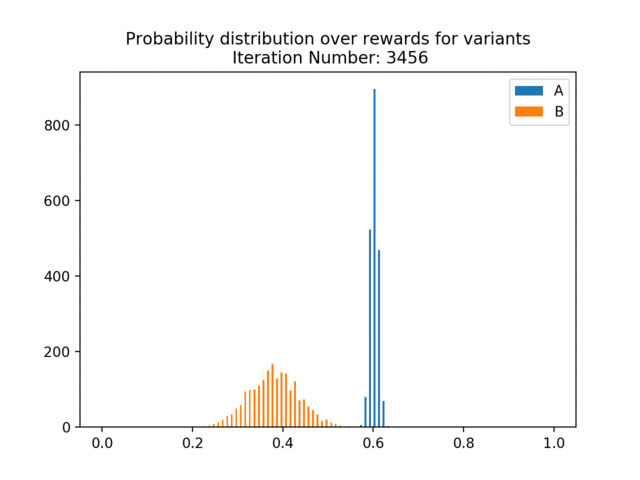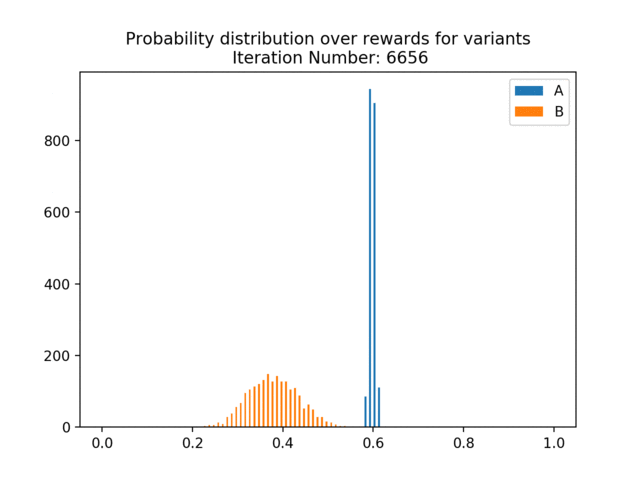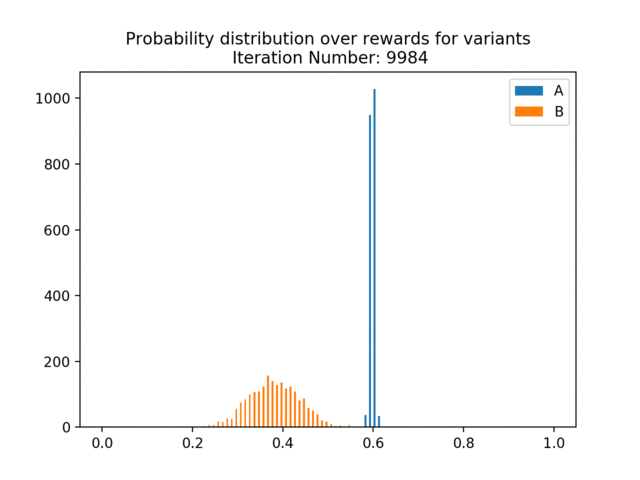
We can also see the regret curve for this data. Regret measures the reward we missed out on from not choosing the optimal variant at each decision point. We know A is better, so regret measures the number of clicks we get relative to always choosing A. We can see that early on, the regret shoots up as we show B relatively often. We are plotting the cumulative regret, so the regret adds up over the course of the experiment. As the experiment continues, the estimated p(click | show A) and p(click | show B) become more peaked and separated and we converge on always showing A — so the regret curve flattens out. This is a very easy example for illustration purposes, where the two variants have very different probabilities of being clicked. Here, the regret curve becomes completely flat much more quickly than we’d expect to see in real-world applications.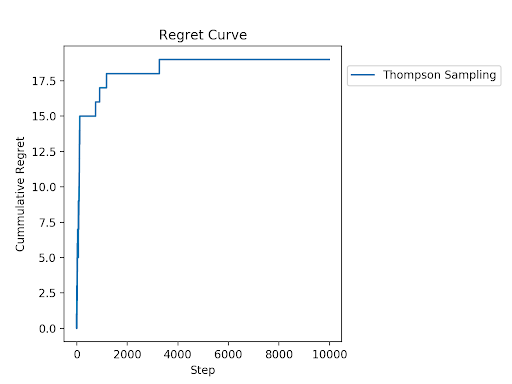

So we can use Thompson sampling to let users set and forget their A/B tests, but in the example above, we still converge on showing only one variant. But when we want to also show variant B to the subset of users who like that best? While Thompson sampling has been around since 1933, this problem creates an opportunity to infuse some deep learning into the process.

Deep Contextual MAB

When we want to learn if a subset of the our users prefers A to B (or vice versa), we can assume there are some features which we’ll denote x that describe the user (such as their country, browser, etc). This means we’d like to learn a function p(click | A, x) and p(click | B, x), or more simply, we want to take into account the user’s features when deciding which variant to show.

An excellent way to model these functions and learn complex “rules” such as if its the weekend, show option A to users from Canada who are using Chrome is by using neural networks. Neural networks allow learning of complex non-linear functions from data without having to encode complex rules.

We simply train a neural network to predict whether a user will click, given the features which describe the user (x) and the variant A/B as input. Neural networks typically output the expectation of this distribution E[p(click | A, x)]. If we simply choose to show A or B based on the expectation, then we might exploit our uncertain knowledge too early. We want to be able to sample from p(click | A, x) in order to do Thompson sampling so we can trade off between exploration and exploitation.

It turns out that to compute p(click | A, x) exactly, or even to sample from the distribution, is intractable (not possible) for deep neural networks. Over the years there have been many attempts to figure out an approximation to this distribution, but these methods typically didn’t scale to large datasets and/or large neural networks.

Fortunately, there’s recently been a great deal of research in “Bayesian deep learning” which has delivered more scalable approximations to this distribution. In particular, a 2015 paper showed that dropout — a very simple and widely used technique to regularize neural networks by randomly shutting off neurons in the neural network — was, in fact, an approximate Bayesian method. Usually, practitioners only used dropout when training the neural network, turning it off when they wanted to make predictions. This paper showed that if you leave dropout on during prediction, you’re getting samples from an approximate posterior distribution — exactly what we need in order to do Thompson sampling.

In addition, a 2017 paper showed that we could learn the dropout probabilities, or the probability of shutting off a neuron. This is called concrete dropout. The cost function to learn the dropout probabilities encourages the network to both be able to predict the data well and give good uncertainty estimates.

So to use neural networks to model p(click | A, x), while simultaneously being able to do Thompson sampling, we simply train a neural network with concrete dropout and leave dropout on at prediction time. When a new user comes in, we input (A, x) and (B, x) into the neural network once, then show the variant that has a higher predicted probability of being clicked on. By doing this, you get the power of neural networks combined with Thompson sampling.

MAB problems where you are also given features about the user (x) are known as contextual MABs, and are widely studied in research literature. But typically, in order to do principled exploration, researchers were forced to use simple linear functions to model the user’s features (x). When practitioners used neural networks for contextual MAB problems, they often used epsilon-greedy strategies to do exploration — but these only explore a random fraction of the time, and thus can easily under- or over-explore.

We at HubSpot know that to learn a good model of how all these features interact with each other, you need powerful non-linear models such as neural networks, which ruled out linear models. And, to maximise our returns, exploration needs to be calibrated carefully, which ruled out epsilon-greedy exploration. Our work combines the simplicity of Thompson sampling with recent advances in Bayesian deep learning so we can use neural networks to model the joint feature — variant space (X, A) — while still getting principled exploration.

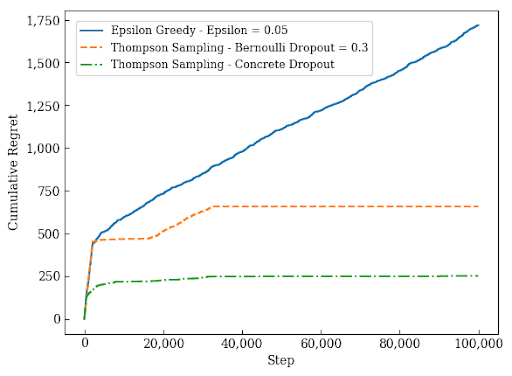
Below is a figure from our paper which shows that our approach using concrete dropout outperforms standard dropout and epsilon-greedy exploration. Not plotted is standard Thompson sampling with no neural network (non-contextual MAB), as this approach incurs cumulative regret of 24,048 compared to the worst-performing method on the figure, which has cumulative regret of 1,718.

Examples where we can simulate a stream of data are ideal, because we can run experiments repeatedly and compare approaches. But in order to make sure our approach is effective in the wild, we also wanted to evaluate it using real, production data.

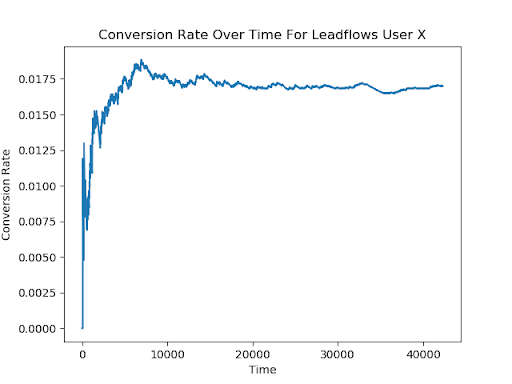
Currently, DCMAB can be used by our Enterprise customers with our Lead Flows tool. The variants involve four different ways to load a pop-up call-to-action onto the screen. Below, we can see the conversion rate over time for one customer who used DCMAB for a Lead Flow. We see that early in the experiment, during the heavy exploration phase, the conversion rate was in the range of 1.0-1.5%. But as the model learned, the average conversion rate climbed and converged to 1.7%. This means our customer got a 0.2-0.7% increased conversion rate by using DCMAB.

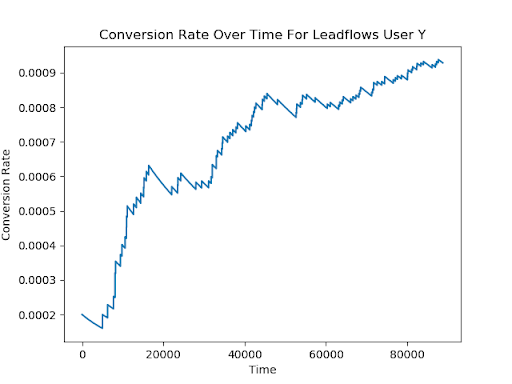
Below, we can see an example from another user, whose initial conversion rate was approximately 0.02%. By the end of the time period, that conversion rate more than quadrupled to 0.09%.

Neat! But what if I don’t know how to train a neural network?

Internally at HubSpot, we have an AutoML tool which automatically builds machine learning models with no human involvement — despite being told nothing about the problem it’s trying to solve. So when you want to use deep contextual multi-armed bandits rather than A/B testing, all the machine learning is automatically taken care of. You get a custom machine learning model trained just on data from your website. The model is periodically retrained as more data rolls in, getting better over time. You don’t have to define the features to use (x), just specify the variants as you would with normal A/B testing.

Through all this work, we now have a fully automatic alternative to A/B testing which is 1) set-and-forget and 2) can learn that subsets of your users may prefer certain variants that standard A/B testing would discard, maximizing the returns from variant testing with no additional effort.

Presently, this tool is offered on a small scale to our Enterprise customers when they use the Lead Flows tool, and we are currently working on rolling out deep contextual multi-armed bandit variant testing to many other areas of the product.

If you’d like to learn more about our approach, we’d love to hear from you. Feel free to leave a message in the comments.